Homework Assignment #5
Due Monday, 12/12

1. Show a neural network that represents the logical function y = (x₁ ∧ x₂) ∨ (x₃ ∧ x₄). Specifically, show the network topology, weights and biases. You should assume that hidden and output units use sigmoid output functions, and an output-unit activation of 0.5 or greater represents a true prediction for y.

2. Consider the concept class C in which each concept is an interval on the line of real numbers. Each training instance is represented by a single real-valued feature x, and a binary class label y ∈ {0, 1}. A learned concept is represented by an interval [a, a + b] where a is real value and b is a positive real value, and the concept predicts y=1 for values of x in the interval, and y=0 otherwise. Show that C is PAC learnable.

3. Consider the concept class that consists of disjunctions of exactly two literals where each literal is a feature or its negation, and at most one literal can be negated. Suppose that the number of features n = 3. Show what the Halving algorithm would do with the following two training instances in an on-line setting. Specifically, show the initial version space, the prediction made by the Halving algorithm for each instance, and the resulting version space after receiving the label of each instance.

   x1	x2	x3	y
   T	F	F	pos
   F	T	T	neg

4. In this same setting, suppose the learner can pick the next training instance it will be given. That is, the learner can pick the feature vector part of the instance; the class label will be provided by the teacher. Which instance should it ask for next? Justify your answer.

5. How many mistakes will the Halving algorithm make for this concept class in the worst case? Justify your answer.

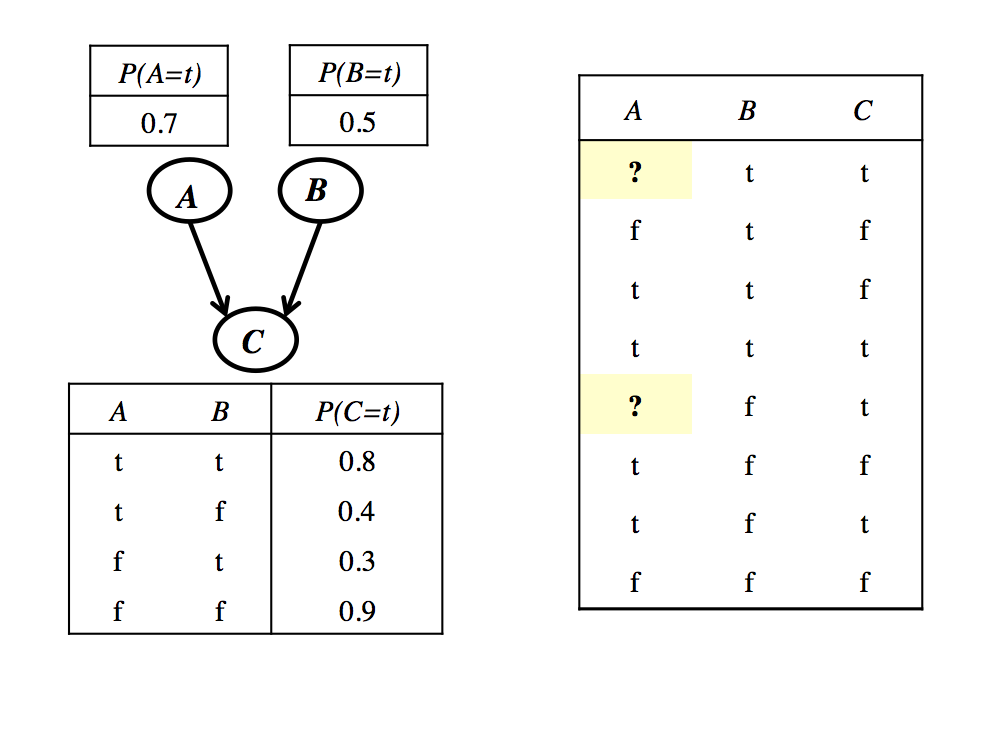
6. Given the initial Bayes net parameters and training set depicted below, show how the network parameters would be updated after one step of the EM procedure. The '?' symbol indicates that the value for the variable A is missing in a given training instance.

   

7. Consider a learning task in which you are given n features and you want to use a feature selection method along with your learning algorithm. Specifically, suppose you are using forward selection along with k-fold cross validation to evaluate each feature set during the search process. Assume that there are r relevant features, and forward selection stops after selecting r features. Given a single training set, how many models are learned in the process of finding a feature subset of size r?

8. Now suppose instead you are using backward elimination for the same task. Again, assume that the search process stops after selecting r features and does not consider feature subsets smaller than this. Given a single training set, how many models are learned in the process of finding a feature subset of size r?

9. Consider the relational learning task defined below. List all of the literals that would be considered by FOIL algorithm on the first step of leaning a rule for the aunt(X, Y) relation.

10. Show the FOIL_gain calculation when sibling(Y, Z) is considered as the first literal to be added to the first rule learning by FOIL. Also show the tuples that are involved in this calculation.

Submitting Your Work